We need a plan that adds up!
Sustainable Energy, without the hot air
This article provides an exposition of techniques for considering reductions of GHG emissions, based on using centibels, a little-known concept for quantifying change.
These alternative techniques, illustrated here through various examples, complement rather than replace the more familiar ones. They provide another perspective on a range of emissions-reduction problems which makes them more straightforward to reason about, in particular by enabling new types of visualizations.
|
There is a companion technical article for readers with a scientific background. |
Introduction
The problem: the environmental transition requires us to make plans with numbers - numbers such as 'GHG emissions must be reduced by 5% every year' or 'the emissions from sea shipping should be halved by 2050'.
Currently, we’re not very good at dealing with such numbers. This guide aims to provide everyone with intellectual tools that make this quantitative planning more straightforward in many situations, while requiring no more than elementary-school math.
The main notion we introduce is the centibel. The centibel (abbreviated 'cB') is a unit of measure for how much some quantity gets scaled or downscaled. Here we will use centibels to quantify variations of GHG emissions and related quantities. It turns out that if we frame our objectives and opportunities in terms of centibels (as opposed to percentages or physical units), many GHG reductions problems become easy to work out and visualize.
Centibels have a use similar to percentages: they describe relative variations. As you can say that some quantity varies by +25% or -50%, so you can say that it varies by +10cB or -30cB. Here are a few more examples:
| Variation | in % | in centibels |
|---|---|---|
×10 |
+900% |
+100.00 cB |
×3 |
+200% |
+47.7 cB |
×1 |
+0% |
+0 cB |
×1.01 |
+1% |
+0.432 cB |
×0.99 |
-1% |
-0.436 cB |
× \$1/2\$ |
-50% |
-30.1 cB |
× \$1/4\$ |
-75% |
-60.2 cB |
× \$1/10\$ |
-90% |
-100 cB |
× \$1/100\$ |
-99% |
-200 cB |
However, centibels don’t work like percentages, because multiplying variations maps to adding the corresponding centibels: for example, dividing a quantity by 2 (-30 cB) then dividing the result by 3 (-48cB) is a (-30) + (-48) = -78 cB reduction. This property of turning multiplications into additions is what makes centibels useful, and percentages have no such property.
We will show you how to concretly convert between percentages and centibels in the Appendix. Meanwhile, the following scale provides a visual reference: [1]

In addition, here are a few more useful reference points:
|
RULES OF THUMB
|
A small amount of practice makes it much easier to convert between centibels and other representations; however, even that is not always needed. As we’ll see, centibels can sometimes be used fruitfully without ever converting them to percentages or physical units, by expressing in the first place the inputs and outputs of the problem at hand in centibels, and letting intuition handle them as it would any other quantity.
Problem: figuring compounded reductions
When asking how much CO₂ is emitted by a given activity, a reasonably accurate answer is often of the form:
The above formula decomposes GHG emissions into 2 factors:
-
GHG intensity: how much GHG we emit by consuming 1 unit of something.
-
also known as the Emission Factor.
-
-
Consumption level: how many units of something are consumed.
Here are some examples of applying the above formula:
| Activity | Consumption level | GHG intensity | GHG emissions | ||
|---|---|---|---|---|---|
Electricity from coal |
10.0 MWh |
\(\times\) |
\(=\) |
10.5 tonCO₂e |
|
Electricity from natural gas |
10.0 MWh |
\(\times\) |
\(=\) |
6 tonCO₂e |
|
Driving a gasoline passenger car |
20 km |
\(\times\) |
\(=\) |
4.6 kgCO₂e |
|
Eating beef |
0.20 kg |
\(\times\) |
\(=\) |
12 kgCO₂e |
The important aspect to us in the above formula is that these factors are combined by a multiplication (not an addition).
This multiplicative relation makes it difficult to figure the overall impact of combining reductions to several factors, because the impact of each reduction depends on the others: we say that the reductions are compounded. For example, when reducing at the same time GHG intensity by -50% and consumption level by -40%, the overall reduction of GHG emissions is not -90% as intuition might suggest, but a more disappointing -70%.
The fundamental problem here is that multiplicative relations are less intuitive to handle and visualize than additive ones. Centibels alleviate that problem, by turning multiplications into additions: -30 cB on GHG intensity combined with -22 cB on consumption level really does yield -52 cB on GHG emissions.
While centibels do make the math easier, their main added value is probably to allow new presentations of the problem, especially visual ones. The basic picture is:

As an example, suppose that you’re a regular meat eater, and want to reduce the GHG footprint of your diet [3]. As is the case for many people, you realize that consuming beef accounts for most of that footprint, and so decide to reduce these beef-related GHG-emissions by a factor of 10 (therefore, a reduction of -90%, or equivalently -100 cB).
To achieve this objective, you have a spectrum of strategies:
-
frugality approach: eating meat 10 times less frequently;
-
efficiency approach: replacing beef with meat that is 10 times less carbon-intensive, such as poultry or pork;
-
a mix of the above 2 approaches.
With that in mind, the following chart displays several diet plans for reducing beef-related GHG emissions:

Note that the above chart is only possible because we are framing the problem in centibels.
Efficiency or frugality?
What must we do to reduce the climate footprint of meat consumption? Should we eat different meat, or should we just eat less meat?
While environmental questions are often framed in such binary terms, polarizing the debate, the previous figure shows us that there is in fact a continuum of possible responses, and gives us more precise answers than a vague "well, we should do both".
|
KEY TAKEWAY When emissions are decomposed into several factors, centibels measure emission reductions evenly across all factors. |
Another common problem is that impressive progress in carbon efficiency can drive us to forget how much of the work must still be done by frugality. In our example, replacing half of beef by poultry feels significant, but attaining our objective still requires eating meat 5 times less frequently [4]. By using centibels, the above figure makes this reality obvious.
|
KEY TAKEWAY Centibels make it easier to plan emissions reductions as a measured combination of efficiency gains and frugality, rather than an unrealistic binary choice between efficiency and frugality. In particular, using centibels tends to reveal the following challenge: even highly-impressive enhancements in efficiency can leave significant work to frugality. |
Diminishing returns
Continuing with our meat emissions example, suppose that you decide to reduce your meat consumption from 10 meat meals per week to only 1. You do so gradually, reducing at each month by 1 meat meal/week:
| Month | Meat meals per week | Reduction from initial consumption |
|---|---|---|
January |
10 |
-0% |
February |
9 |
-10% |
March |
8 |
-20% |
… |
… |
… |
September |
2 |
-80% |
October |
1 |
-90% |
November |
1 |
-90% |
The September→October transition prevents exactly the same GHG emissions as the January→February transition: those of 1 meat meal per week, that is 10% of the initial emissions level.
Yet there is a sense in which the September→October transition is much harder than the January→February transition, because the former is a much more drastic reduction in the frequency of meat meals:
| Transition | from | to | gives up on |
|---|---|---|---|
January → February |
-0% |
-10% |
1 in 10 meat meals |
September → October |
-80% |
-90% |
1 in 2 meat meals |
In other words, in a -90% reduction trajectory, eliminating the first 10% of emissions is usually much easier than eliminiting the last 10%. This applies to a broad spectrum of domains, especially when the reductions consist of improving the efficiency of some process. Centibels are effective at making obvious such differences in relative variations:

The above figure also illustrates the main shortcoming of centibels: the reduction in centibels is not proportional to the reduced emissions. As we progress along the reduction path, progressing by -1cB achieves less and less in terms of reduced tonnage of CO₂, whereas progressing by -1% always means eliminating one 100th of initial emissions.
Therefore, centibels are usually a better proxy of reduction cost than of reduction impact.
Having said that, this shortcoming is not always a huge loss. One of the lessons of this section is that it makes little sense to ask for the CO₂ impact of a reduction action when it’s compounded with others (How much CO₂ does it save to halve carbon intensity? Well, it depends on how the consumption level evolves).
Application: decomposing the reduction effort across factors
When GHG emissions result from several compounded factors, using centibels makes it straightforward to reason about reducing them. This is illustrated in the following section by considering emissions from cement production.
Example: reducing emissions from cement
Assume that we want to reduce the CO₂ emissions from producing cement for construction: for example, we might aim to divide these emissions by 10 (-90%) on the long term, which corresponds exactly to a -100 cB target.
To model cement-production GHG emissions, we decompose them into the following factors:
-
CO₂ intensity: how much CO₂ is emitted from producing a ton of cement. (in tonCO₂eq/t)
-
Influenced by: production technology.
-
-
Construction density: how much cement we use per building area (in t/m²).
-
Influenced by: architectural design.
-
-
Usage: how much we build (in m²).
-
Influenced by: housing policies, lifestyle choices.
-
To be more explicit: in this model, CO₂ emissions are given by the following formula:
When using centibels, the above equation turns into the 'budget problem' of splitting the -100cB reduction across our 3 factors. The following chart provides an example:

|
KEY TAKEWAY When expressed in centibels, emissions reduction objectives become a 'budget' problem: how many centibels are contributed by each factor. This is not possible with percentages or tonCO₂eq, because the reductions on individual factors are compounded. |
Application: emissions reduction pathways
The previous section discussed allocating emissions reduction efforts over several factors. This one discusses allocating them over time, that is planning emissions reduction pathways. Here again, framing the problem in centibels can make it more workable.
Case study: to have a good chance of limiting global warming to less than +2°C, we decide starting from now to reduce GHG emissions at a rate of -6.4% every year.
By how much will we have reduced GHG emissions in 10 years?
Most people will either tell you that they don’t know, or give the instinctive but incorrect answer of -64%. Those few who can find the correct formula of \(100 \times \left(1 - \left(1 - \frac{6.4}{100}\right)^{10}\right)\) probably cannot compute it off the top of their heads. The fundamental issue here is that successive applications of percentages is tricky.
On the other hand, if we frame our objective as
We will reduce our GHG emissions by -2.89 cB/year
anyone can tell that in 10 years, we will have reduced them by -28.9cB, from which you can quickly translate it to a -49% reduction. In centibels, the correct calculation is the intuitive one.
The advantage of centibels is even more evident when we reverse the problem:
If we aim for -48% GHG emissions in 10 years, by what fraction must we reduce them each year?
At this point, only the scientifically trained have a chance of finding the correct formula of \(100 \times \left(1 - \left(1 - \frac{48}{100}\right)^{\frac{1}{10}}\right)\). On the other hand, if I tell you that we aim for -28.4 cB in 10 years, you can easily tell that this translates to a reduction of -2.84 cB/year.
|
KEY TAKEWAY Successive applications of percentages are arithmetically hard. Most people get them wrong. In contrast, for same purpose, centibels require only basic additions and subtractions, the kind of which we use for everyday accounting. |
How many centibels per year?
We mentioned a 'speed of decline' of GHG emissions of -2.89 cB/year. This section explains how to compute such a number.
At the time of writing, it is estimated that the world has a remaining 'emissions budget' of 646 GtCO2e to stay below +2°C of global warming.
Emissions reduction pathways are designed so as to not emit more than this 646 GtCO2e threshold in the future: the 'speed of decline' is computed accordingly, depending on when we start reducing emissions (the more we delay, the faster we will have to reduce emissions). The mathematics of the problem are too involved to derive here, but they yield the following rule:
Working out the required 'speed of decline' of GHG emissions, in cB/year:
-
If we kept our current yearly emissions of 42.1 GtCO2e/year, we would have exhausted our 646 GtCO2e carbon budget in 2036. Let’s call 2036 the Pivot Year for global emissions.
-
Constraint: we must have reduced emissions by -43.4 cB at the Pivot Year. (-63.2%)[5]
So if we started reducing in 2021, this would mean a reduction of -43.4 cB in 15 years, i.e -2.89 cB/year (-6.45% every year).
If we delayed by 5 years and started reducing in 2026, this would be a much more challenging -4.34 cB/year (-9.52% every year).

|
KEY TAKEWAY Exponential-decay pathways, one of the most commonly used type of trajectories for communicating about emissions reduction, are easy to reason about in centibels: we remove the same number of centibels every year. Thanks to the "-43.3 cB at Pivot Year" rule, it’s easy to keep track of the rate at which to reduce emissions (and how it grows as we delay). |
|
The specific shape of the pathway is critical
The above 'target' of -43.4 cB only applies to 'constant centibels speed' reduction pathways (which consist of reducing emissions by the same numbers of centibels every year - known in the scientific community as exponential decay pathways). If the curve of our emissions doesn’t follow rigourously this specific shape, especially in early years, this rule no longer works. For example, in order to account for 'inertia' in yearly emissions, another approach is to plan reductions not at 'constant centibels speed', but at 'constant centibels acceleration': emissions then follow a 'half-bell curve' with a slower decline in early years and a more brutal 'landing' in late years. In this case, the Pivot Year target is -34.1 cB[6]; starting the reductions in 2021 would then require an 'acceleration' of -0.303 cB/year². |
|
Emissions budgets may vary by country or sector
For various reasons ranging from equity to practicality, it might be sensible that emissions budgets not be distributed uniformly among countries or industrial sectors. This implies different decarbonization speeds and Pivot Years across countries and sectors. |
|
Negative emissions
Some emission pathways plan for GHG emissions to become negative after a few decades. Centibels cannot handle negative quantities, and so are not suitable for modeling such pathways. |
Application: the Kaya equation
The Kaya equation describes the GHG emissions of a society by decomposing them into the following 4 factors:
The factors are:
-
\(\text{Pop}\): the population size (in persons)
-
\(\frac{\text{GDP}}{\text{Pop}}\): the GDP per capita (in $/person)
-
can be loosely interpreted as the average "standard of living" (how much economic production each person enjoys on average), with important caveats in said interpretation.
-
-
\(\frac{E}{\text{GDP}}\): the energy intensity of economic production (in kWh/$)
-
in English: how much energy is needed to produce $1 of added value (on average).
-
-
\(\frac{\text{GHG}}{E}\): the carbon content of energy (in gCO₂eq/kWh)
-
in English: how much CO₂ is emitted when consuming 1kWh of energy (on average).
-
Because the Kaya equation is a multiplicative chain, we can gain insights by discussing it in terms of centibels. Concretely, if we aim to reduce GHG emissions at a pace of -2.89 cB/year, then all 4 factors must vary each such that their variations sum to -2.89 cB/year.
Importantly, if some of the 4 factors are increasing rather than decreasing, then they play adversarially to reducing GHG emissions, adding to the burden on the other factors.
For example, if GDP per capita increases by +1 cB/year, then the burden of reduction on the other 3 factors is now -3.89 cB/year. Likewise, a growing population adds to the challenge of reducing GHG emissions. This is illustrated in the following figure:

Today, when discussing the environmental transition, the first two factors get most of the attention. For example, replacing fossil fuels with renewable or nuclear energy sources reduces \(\frac{\text{GHG}}{E}\). Likewise, making our economy more energy-efficient (for example: replacing air travel with train travel, enhancing the fuel economy of cars, replacing radiators with heat pumps, or redirecting our leisure expenses from watching online video to reading books) reduces \(\frac{E}{\text{GDP}}\).
You might think that achieving a fast pace of reduction on \(\frac{\text{GHG}}{E}\) is easy, thanks to renewable energy sources: after all, the carbon content of wind electricity is a good -100 cB below that of coal, even when accounting for storage. But this analysis overlooks the following issues:
-
Electricity production only accounts for about 40% of GHG emissions, and electrifying the other energy uses is much more work than just replacing power plants.
-
The sheer scale of the electicity production to substitute is challenging in itself, posing in particular difficulties of material supply.
-
About 30% of GHG emissions are not related to energy consumption at all (in particular from agriculture, as well as the cement and metallurgy industries).
Can we do something about \(\frac{E}{\text{GDP}}\), i.e make our economies less energy-intensive? To some extent, we’re already doing it: for example, some estimations show that \(\frac{E}{\text{GDP}}\) has decreased at a pace of -0.8 cB/year from 2005 to 2015 at the global level[7].
People and governments tend to have strong feelings about demographic policies and economic growth; we will not debate here what objectives are acceptable regarding these factors, but it’s important not to forget that they exist and can exert strong influence on GHG emissions, for better or for worse.
Application: handling more advanced emissions models
Some situations demand more sophisticated emissions models than an elementary multiplication of factors, because some of the factors have to be raised to a certain power. These emissions models, known as power laws, are typically not discussed outside of technical circles, due to their relative mathematical sophistication. As we’ll see, using centibels can make it easier to reason about such models.
Example: saving fuel on cargo ships
You might have heard that a cargo ship consumes less fuel when it goes more slowly, which reduces GHG emissions.
However, reducing the speed of a cargo ship also reduces the throughput at which it delivers goods, and so reducing speed will increase the number of cargo ships at sea, which increases GHG emissions.
Can we tell which effect will win out? Can we reduce GHG emissions by changing the speed of cargo ships?
We have the following formulas for transportation throughput and GHG emissions:
in which \(A\) and \(B\) are constants which won’t matter to us here.
From these formulas, any engineer can give you the following elements:
-
Increasing fleet size by +1 cB will increase both throughput and GHG emissions by +1 cB
-
Decreasing ship speed by -1 cB will decrease throughput by -1 cB and GHG emissions by -3 cB
From here, you can deduce that by trading -1 cB in ship speed for +1 cB in fleet size, you keep the same transportation throughput, while reducing GHG emissions by +1 -3 = -2 cB.
| Action | Impact on throughput | Impact on GHG emissions |
|---|---|---|
-1 cB speed |
-1 cB |
-3 cB |
+1 cB fleet size |
+1 cB |
+1 cB |
Both actions |
+0 cB |
-2 cB |
So the answer is: yes, reducing ship speed does reduce GHG emissions in spite of the increase in fleet size (hurray!). Notice that by framing the situation in terms of centibels, we made this opportunity easy to spot and work out.
For example, you can verify that a -10cB reduction in speed compensated by a +10cB increase in fleet size would translate to -20.6% in ship speed, +25.9% in fleet size, and -36.9% in GHG emissions from fuel consumption. In addition, compounding this approach with a frugality policy, we might not compensate all the way to +10cB in fleet size, in which case the GHG emissions would be even more reduced.
Of course, such a change would have drawbacks: for example personel costs would increase and sea voyages would last longer. But this is typically the sort of tradeoffs to be considered for the environmental transition.
|
KEY TAKEWAY In some situations, the impact of reduction actions can become much easier to work out when quantifying them in centibels. |
Conclusion
Centibels are a conceptual tool for considering changing quantities. As such, they play a role similar to percentages, but bring different insights. We find that centibels add a useful perspective on reducing GHG emissions.
Centibels are valuable in situations where GHG emissions are broken down into compounded factors, rather than distributed over separate sectors.
In particular, centibels make more tangible the continuum of possibilities between frugality-only and efficiency-only emissions reductions. If this leads (as we hope) to more constructive and less polarized discussions about what the carbon transition involves, that will likely be their most useful application.
Centibels represent compounded reduction actions as additive contributions with a shared unit of measure. Reducing emissions can then be viewed as a budget allocation problem.
Some emissions reduction problems, when framed in centibels, become more straightforward to think about.
We hope it’s clear that centibels are not an emissions-reduction technology. They add nothing to the set of concrete reduction actions available to us, and can only help by making us more lucid about orchestrating them.
Appendix: converting to / from centibels
Denoting \(p\) the relative percentage (e.g -75%), \(s\) the corresponding scaling factor (e.g \(\times \frac{1}{4}\)), and \(c\) the corresponding centibels (e.g -60.2 cB), we have the following conversion formulas:
Note that the first and last formulas are merely reminders about what relative percentages mean.
Here are screenshots of converting between centibels and relative percentages on the calculator app of an Android phone:
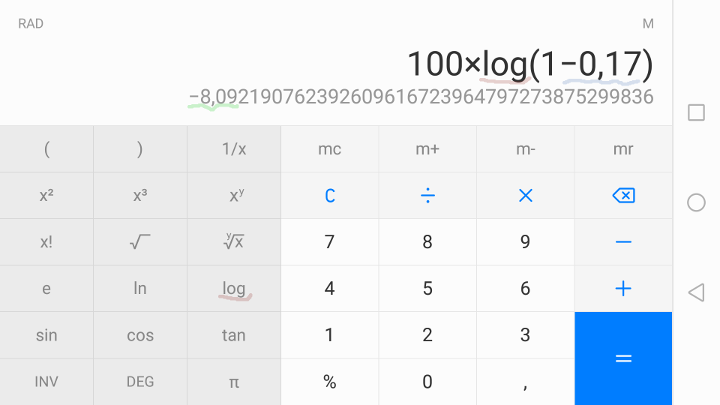

Note that some computations involve a \(\log\) function (pronounce: "logarithm"). There exist several logarithm functions; to make sure you’re using the correct one[8], verify that \(\log(10) = 1\).
Appendix: on the implicit use of logarithms
Some knowledgeable readers might be surprised that the word 'logarithm' never appears in the body of this article. Indeed, logarithms are essential to centibels, and the companion technical article is very explicit about this. When writing the present article, we made this omission deliberately, in order to prove a point: that most of the benefits of logarithmic representations can be reaped without any formal understanding of their mathematical foundations, the key substitute being the centibel unit of measure. There are a few historical precedents: the pH for acidity, the Richter magnitude scale for earthquakes, and of course the decibel, mostly used for sound, are all logarithmic units in common use.
Many of the centibel-based graphics in this article are visually equivalent to using a logarithmic scale on some axis. The advantage of centibels over logarithmic scales is that they convey meaning which extends outside of the graphics. For non-scientific audiences, logarithmic scales usually demand to be complemented by an explanation anyway.
About the authors

Valentin Waeselynck is an independent software engineer and data scientist, with an interest in technical pedagogy.
He graduated in Engineering from the École Polytechnique.

Pauline Vialatte currently manages environmental projects at the French Development Agency of Santo Domingo, after several years working as a Climate/Energy consultant and carbon offset project developer at EcoAct.
She graduated in Engineering at Institut d’Optique Graduate School, and in Sustainable Development at HEC Paris.